Dibujos con funciones matemáticas
Hace poco me hicieron un desafío a través de Twitter:
Podrá @kouta5428 hacer algo asi? Con una carita feliz me conformo https://t.co/XomATFnBNW
— Rodion R. Raskolnikov 🇺🇾 ☭ (@aastrikesagain) November 4, 2024
Me deben decir Bob el Constructor de la forma en que sí podemos. Full disclaimer: no vamos a dibujar una hermosa aguaviva; vamos a dibujar una carita feliz.
Primero, utilizando Desmos, podemos encontrar ecuaciones que dibujen una forma:
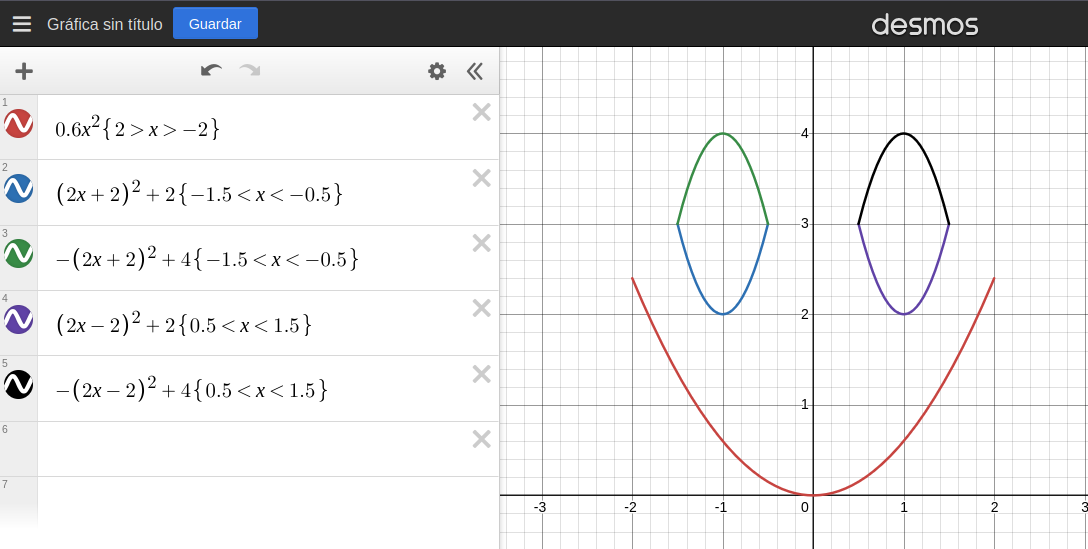
Dibujando una cara en Desmos
Con estas 5 expresiones, podemos dibujar una cara:
\[ 0.6x^{2} \{2>x>-2\} \]\[ (2x+2)^{2}+2 \{ -1.5 < x < -0.5 \} \]\[ -(2x+2)^{2}+4 \{ -1.5 < x < -0.5 \} \]\[ (2x-2)^{2}+2 \{ 0.5 < x < 1.5 \} \]\[ -(2x-2)^{2}+4 \{ 0.5 < x < 1.5 \} \]¿Listo? Y, no. Esto tiene varios problemas.
- Son varias expresiones, no una.
- Estas expresiones dibujan sólo una parte de la imágen
- Cada expresión es una expresión definida por tramos, y dibuja un punto a la altura del X que se le aplique.
Lo que nosotros queremos es una única expresión, que dado un punto (x,y) nos devuelva el valor del pixel en ese punto. Vamos a asumir que nuestra imágen es un bitmap monocromático, para lo cual querremos que estas expresiones devuelvan 0 en los (x,y) donde no dibujen y 1 en los (x,y) donde sí dibujen. Podemos lograr esto mediante la multiplicación de 2 condiciones:
- La cercanía de \( y \) al valor de la expresión en el punto x: \( (y - f(x)) < \epsilon \)
- La partenencia de \( x \) al tramo \( [minX; maxX] \) al que está limitada la expresión: \( minX < x < maxX \)
Ambas de estas condiciones pueden implementarse a través de una expresión común que devuelve 1 para los valores de X entre \( [A; B] \) y 0 para los valores de X fuera de \( [A; B] \):
\[ \displaylines{c := \frac{(a+b)}{2} \newline d := \frac{b-a}{2} \newline isin(x) = max(0, ceil(-(\frac{abs(x-c)-d}{d}))) }\]Podemos validar esto utilizando Desmos:
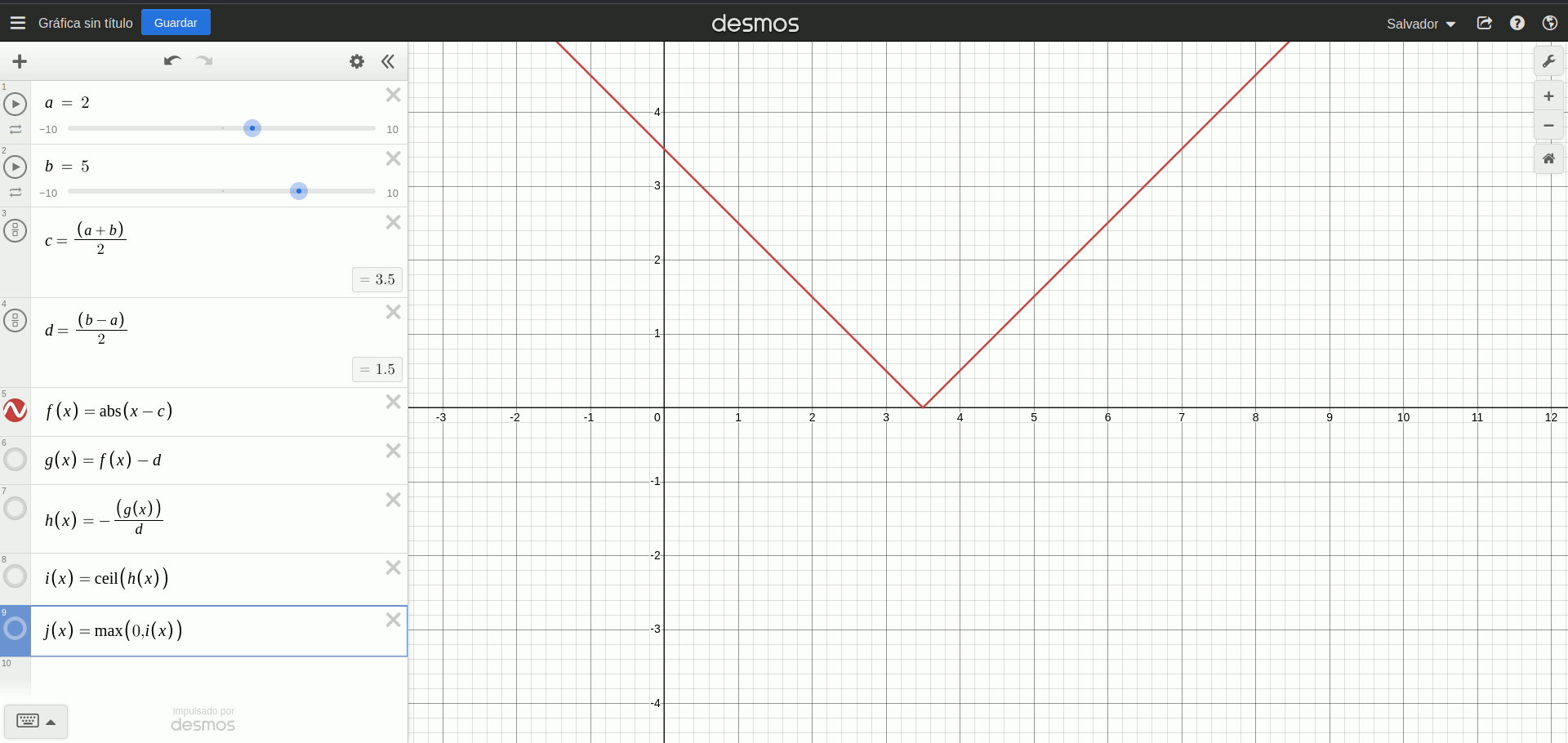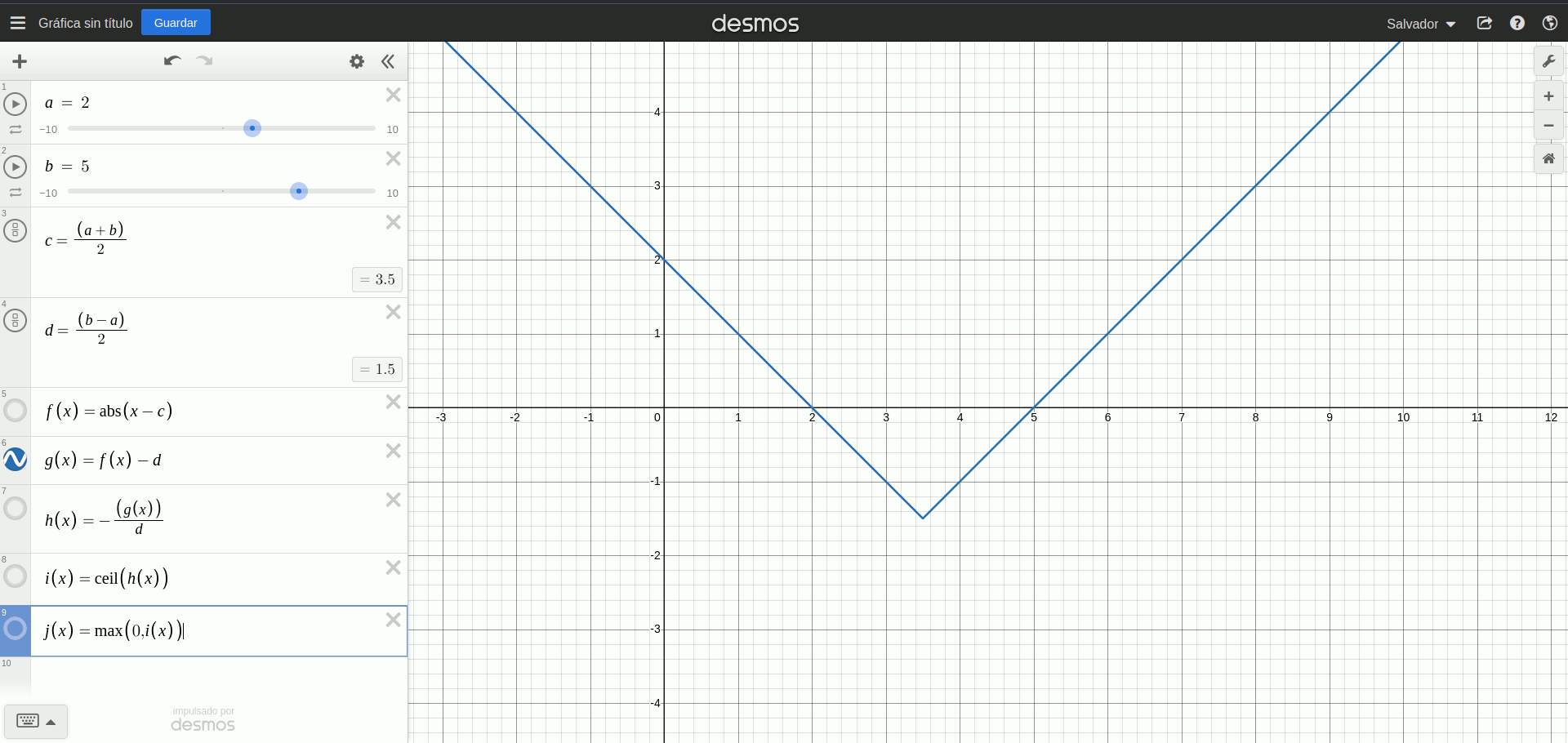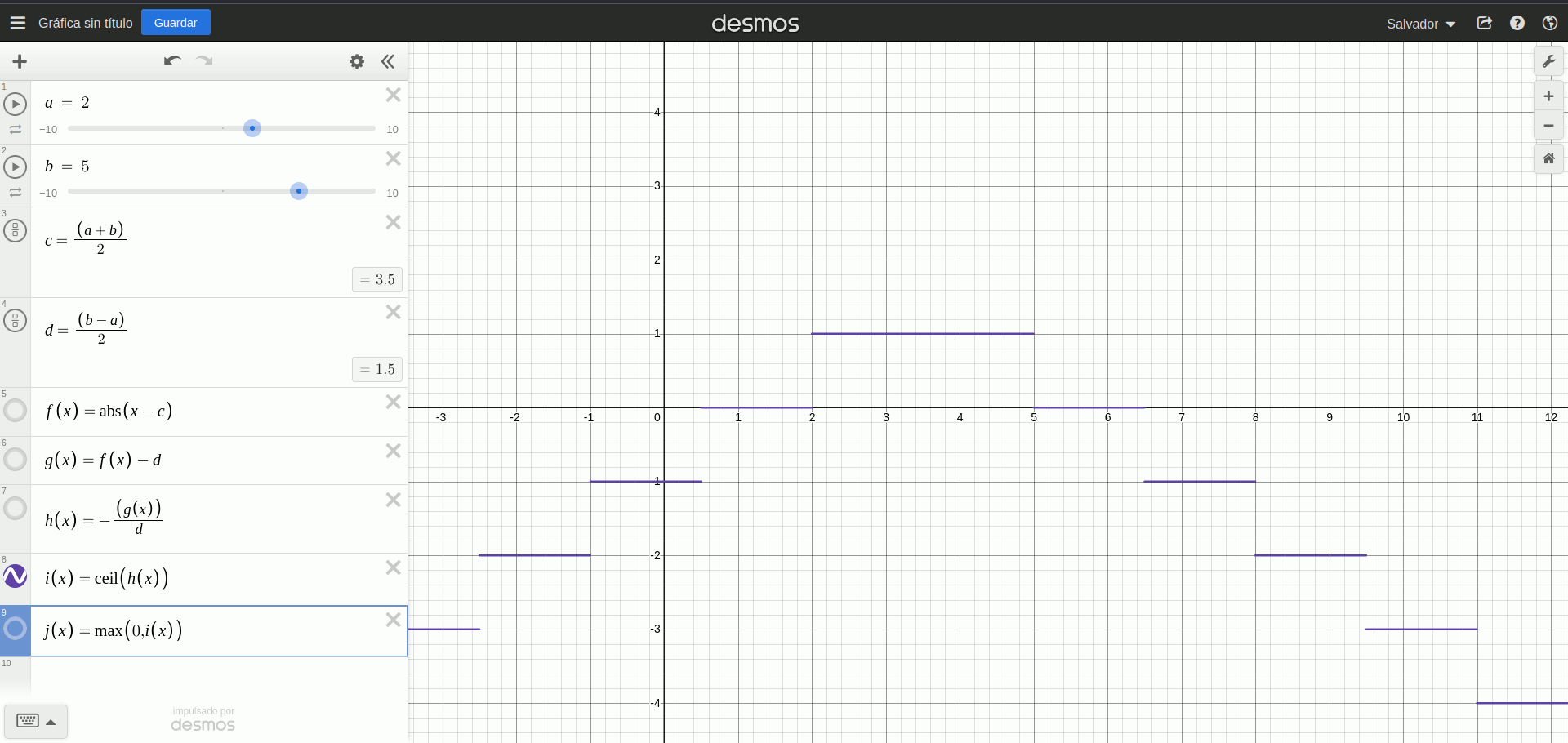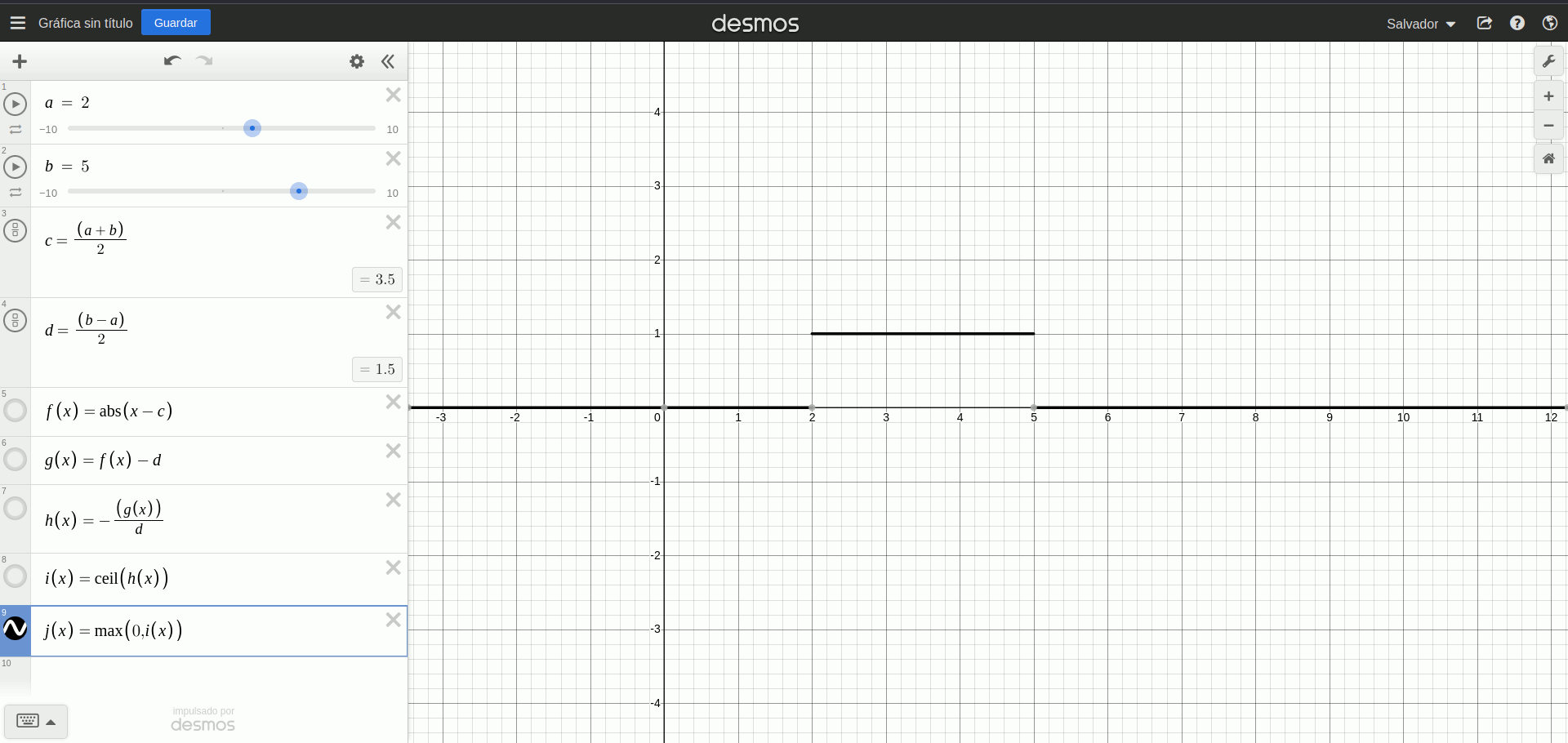
isin(x)
Me costó lograr una interpretación de por qué esta expresión funciona, y lo que puedo ver es que:
- Centra la función en C (punto medio de [A;B]) y saca el absoluto para calcular la distancia entre X y C
- Resta D (ancho del intervalo [A;B]) para que los valores de X que están a menos de D de distancia de C (es decir son parte de [A;B]) sean negativos
- Niega el valor y lo divide entre D, para que los valores de X que están en el intervalo sean positivos y estén entre 0 y 1
- Aplica ceiling(x) para que todos los valores entre 0 y 1 sean 1
- Limita a 0 para que ningún valor sea distinto a 0 o 1
Con lo cual podemos ver que efectivamente isin(x) devuelve 0 cuando X no es parte del intervalo [A;B] y 1 cuando sí lo es.
Utilizando isin(x) podemos implementar ambas condiciones:
- \( (y - f(x)) < \epsilon \) se convierte en \( isin(x) \) con \( A = f(x) - \epsilon \) y \( B = f(x) + \epsilon \)
- \( minX < X < maxX \) se convierte en \( isin(x) \) con \( A = minX \) y \( B = maxX \)
Por ejemplo, para la primera expresión \( 0.6x^{2} \{2>x>-2\} \):
- La definición de tramo expandiendo
isinse transforma en \( max(0, ceil(-(\frac{abs(x)-2}{2}))) \) - La cercanía del Y al valor de F(X) se transforma en \( max(0, ceil(-(\frac{abs(y - \frac{(0.6x)^{2} - \epsilon + (0.6x)^{2} + epsilon}{2}) - \frac{((0.6x)^{2} + \epsilon - ((0.6x)^{2} - \epsilon))}{2}}{\frac{(0.6x)^{2} + \epsilon - (0.6x)^{2}-\epsilon}{2}}))) \)
- Ambas expresiones devuelven 0 o 1 dependiendo de si se cumple su expresión, por lo cual la función \( smile(x,y) \) es la multiplicación de ambas expresiones: \[ max(0, ceil(-(\frac{abs(x)-2}{2}))) \times max(0, ceil(-(\frac{abs(y - \frac{(0.6x)^{2} - \epsilon + (0.6x)^{2} + epsilon}{2}) - \frac{((0.6x)^{2} + \epsilon - ((0.6x)^{2} - \epsilon))}{2}}{\frac{(0.6x)^{2} + \epsilon - (0.6x)^{2}-\epsilon}{2}}))) \]
Podemos validar esto haciendo código en Python (algún día lo subiré a Github):
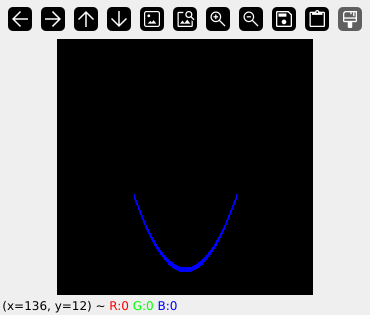
smile(x,y)
Como podemos ver, la función smile(x,y) devuelve 1 en los puntos que pertenecen a la curva de la primera expresión, y 0 en aquellos que no.
La función final que combina todas estas expresiones sería la suma de todas las expresiones limitada a 1 (no podemos tener un canal con valor mayor a 255 :D). Como el desarrollo manual de las expresiones es demasiado tedioso, la función final se desarrolló utilizando la librería SymPy de manipulación simbólica, la cual además aplica simplificaciones que acortan las expresiones.
\[ \displaylines{ \max\left(0, \left\lceil{- 0.5 \left|{x}\right|}\right\rceil + 1\right) \max\left(0, \left\lceil{- 20 \left|{0.36 x^{2} - y}\right|}\right\rceil + 1\right) + \newline \max\left(0, \left\lceil{- 2 \left|{x - 1}\right|}\right\rceil + 1\right) \max\left(0, \left\lceil{- 20 \left|{- y + 4 \left(x - 1\right)^{2} + 2}\right|}\right\rceil + 1\right) + \newline \max\left(0, \left\lceil{- 2 \left|{x - 1}\right|}\right\rceil + 1\right) \max\left(0, \left\lceil{- 20 \left|{y + 4 \left(x - 1\right)^{2} - 4}\right|}\right\rceil + 1\right) + \newline \max\left(0, \left\lceil{- 2 \left|{x + 1}\right|}\right\rceil + 1\right) \max\left(0, \left\lceil{- 20 \left|{- y + 4 \left(x + 1\right)^{2} + 2}\right|}\right\rceil + 1\right) + \newline \max\left(0, \left\lceil{- 2 \left|{x + 1}\right|}\right\rceil + 1\right) \max\left(0, \left\lceil{- 20 \left|{y + 4 \left(x + 1\right)^{2} - 4}\right|}\right\rceil + 1\right) } \]Al ejecutar esta función para todas las combinaciones de X en \( [5.0;-5] \) e Y en \( [4.5;-0.5] \) recibimos esta imagen:
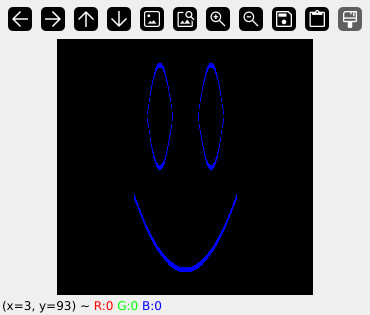
smile(x,y) + left_eye_bottom(x,y) + left_eye_top(x,y) + right_eye_bottom(x,y) + right_eye_top(x,y)
Existirían varias mejoras posibles, como por ejemplo desarrollar funciones distintas para cada canal de color permitiendo mezcla de colores, etc. Pero hasta acá llegó mi interés por los dibujos matemáticos.
(Después subo el código a Github)